Understanding process capability in statistical process control

Brad J. Thacker, DVM, PhD, MBA, Diplomate ABVP

Intervet Inc, 903 Park Circle, Huxley, IA 50124; E-mail: brad.thacker@intervet.com.

Cite as: Thacker BJ. Understanding process capability in statistical process control. J Swine Health Prod. 2005;13(1):53-55.

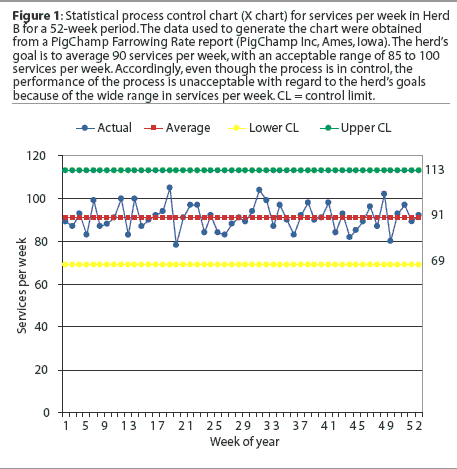
Statistical process control chart (X chart) for services per week for a 52-week period in Herd B. The service target for this herd is 90 per week. In the chart, the six-sigma control limits (CL) are 69 and 113, ie, any value between 69 and 113 is within the control limits (CL). In this herd, is the process for managing services per week effective? Is the process capable of meeting herd goals?

Statistical process control charting (SPCC) has become a popular method for analyzing swine production data. In most cases, the data is captured by computerized recording systems such as PigChamp (PigChamp Inc, Ames, Iowa), and the summary information generated from these programs is exported into other programs for generating SPCC graphs. Several types of SPCC routines are available, and the choice of which routine to use is based primarily on the type of data analyzed.

For production data that is generated on a weekly or group basis, the X chart (sometimes called I chart) is most useful. With the X chart, process variability is derived from the moving range, which is the difference between two successive observations. Examples of appropriate data for X charting include farrowings per week, services per week, pigs weaned per week, and rate of gain per group. X charting can be used for proportional data such as farrowing rate and mortality, although P charts are perhaps more appropriate for proportional data because the denominator (eg, services per week) for each individual rate (eg, weekly farrowing rate) is incorporated into the calculations used to generate the chart. This may be important if the denominator is highly variable.

The goal of SPCC is to identify situations where the process is out of control, as evidenced by increased variability in process behavior. Simply stated, the process is judged to be out of control when the data generated from the process and evaluated by SPCC exceed limits that are either specified by the evaluator or determined by previous data generated from the process. In most cases, using the data generated from the process is the most appropriate method for determining the upper and lower control limits. In general, the upper and lower control limits represent a range of six standard deviations (SDs) or six sigma around the average performance of the process. In addition, evaluation of data trends is considered (eg, a series of increasing or decreasing values or a number of consecutive values above or below the average performance). In this regard, SPCC is used to determine if the process is behaving abnormally, as evidenced by increasing variability or unexpected patterns.

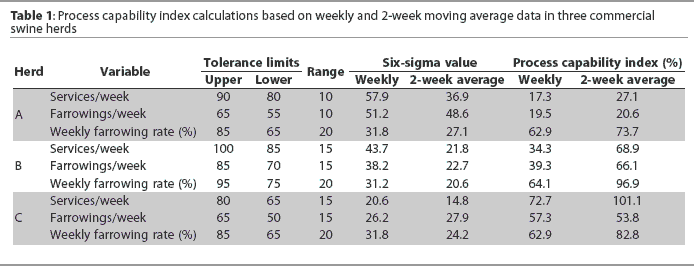
One aspect of SPCC that is rarely addressed is the concept of process capability. Often, data such as services per week are charted, and the chart does not disclose any values that suggest the process is behaving abnormally (ie, all points are within the six-sigma limit). On the other hand, the range of values generated is unacceptable with respect to the operation’s goals. Figure 1, which depicts services per week for a 52-week period, provides an example of this. The service target for this herd, designated Herd B, is 90 per week. The chart indicates that for the 52-week period, the average number of services per week was 91, while the six-sigma control limits were 69 and 113. Accordingly, any value between 69 and 113 would be within the control limits. This range is much wider than the desired range of 85 to 100, as shown in Table 1. One could argue that our process for managing services per week is in control, but the process is not capable of meeting our goals.

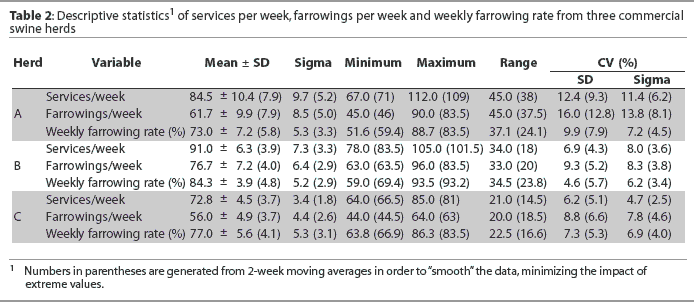
In order to provide examples of field data for analysis, PigChamp records from three herds were used. A farrowing rate report was generated for 52 weekly periods. The report was then imported into Excel (Microsoft Corp, Redmond, Washington) and formatted for import into Statistix (Analytical Software, Tallahassee, Florida), which was then used to generate summary data (means, SDs, and ranges) and control charts (sigma values). Table 2 presents data based on raw weekly values from the three herds. In addition, data in parentheses were generated from 2-week moving averages in order to "smooth" the data so that extreme values have less impact on our evaluation. The justification for smoothing is based on the ability of herd managers to adjust flow through the farrowing barn by altering lactation length or wean age. For all values, using the 2-week moving average decreased variability, as measured by SD, sigma, range, and coefficient of variation (CV).

Process capability depends on the behavior of the process (voice of the process) and the goals of the manager (voice of the customer). In Table 1, ranges of acceptable behavior are presented as tolerance limits. These limits vary by herd on the basis of herd or service group size, lactation length or wean age, weaning days per week, and percent planned overfarrowing. For example, Herd A has a tighter tolerance, because lactation length is lower than in Herd B, and Herd A weans once a week and overfarrows at a rate of 5 to 8%. Herd B does not overfarrow and Herd C weans three times per week. Setting tolerance limits is more art than science at this point, as variables that may affect the limits to select are numerous but not well documented mathematically. On the other hand, most goals with regard to flow variability in a breeding herd are not aligned with the processes in place and are therefore too optimistic.

The process capability index (PCI) is calculated from the behavior of the process and the tolerance limits that we have established. The PCI for farrowings per week (using the 2-week average calculation method) for Herd A is only 20.6%, due to low PCI for services per week (27.1%) and intermediate farrowing rate (73.7%). Herd C’s PCI is intermediate for farrowings per week (53.8%), even though farrowing rate PCI is intermediate (82.8%) and the PCI for services per week is > 100%. Herd B has the highest PCI (66.1%) for farrowings per week, mainly because the PCI for farrowing rate is high (96.9%), while the PCI for services per week is intermediate (68.9%). It appears, in comparing these three herds, that PCI for farrowing rate per week has a larger impact on PCI for farrowings per week, while the impact of PCI for services per week is less important. Other studies have suggested that services per week is more important. However, one can argue that none of the herds are performing at an acceptable level with regard to farrowings per week, because even the best herd’s PCI for farrowings per week (Herd B) is only 66.1%. Furthermore, variability in farrowings per week will inevitably lead to variability in number of pigs weaned, weaning weights, or both, as impacted by weaning age.

The overarching utility of SPCC charting is to help differentiate variation due to "special causes" versus the normal "background" variation inherent in any process. The PCI measures the relative ability of the process to meet the objectives of the manager. If the process behaves normally within the six-sigma boundaries, but fails to meet process goals, then all aspects of the process need to be evaluated, rather than taking a narrow focus on a few suspected deficiencies. In other words, all aspects of the process should be questioned. An old saying that has considerable utility in managing any business is "Plan your work and work your plan." In SPCC terms, one could substitute the following: Develop a process that is capable of meeting your objectives and then monitor for special causes of variation by SPCC. All too often, a process is monitored by SPCC without sufficient knowledge or evaluation of process capability. Accordingly, the voice of the process becomes discordant with the voice of the customer.